| value of x: | value of y: (which is 2x) |
| x= -2, then | y= -4 (because 2 x -2 = -4) |
| x= -1, then | y= -2 (because 2 x -1 = -2) |
| x= 0, then | y= 0 (because 2 x 0 = 0) |
| x= 1, then | y= 2 (because 2 x 1 = 2) |
| x= 2, then | y= 4 (because 2 x 2 = 4 |
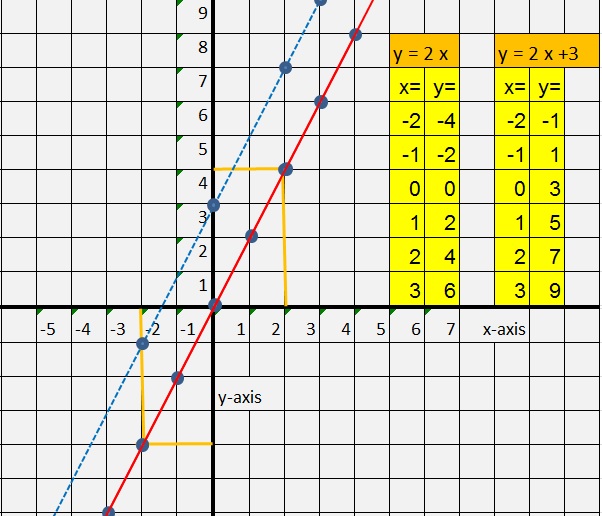
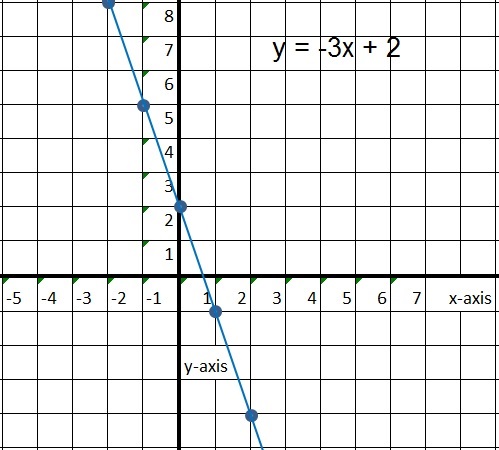
| value of x: | value of y: (which is -3x + 2) |
| x= -2, then | y= 8 (because -3 x -2 + 2 = 6 + 2 = 8) |
| x= -1, then | y= 5 (because -3 x -1 + 2 = 3 + 2 =5) |
| x= 0, then | y= 2 (because -3 x 0 + 2 = 0 + 2 = 2) |
| x= 1, then | y= -1 (because -3 x 1 + 2 = -3 + 2 = -1) |
| x= 2, then | y= -4 (because -3 x 2 + 2 = -6 + 2 = -4 |
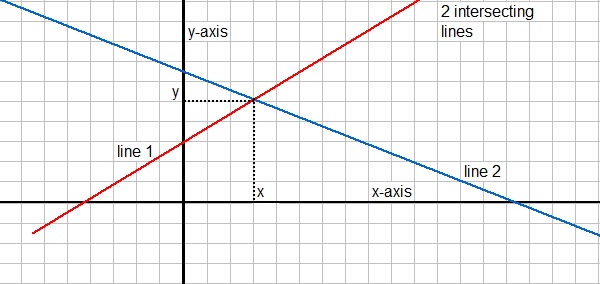
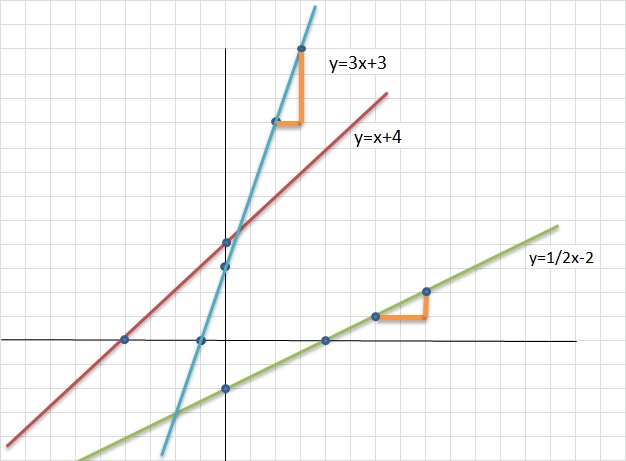
| slope= |
4 - 1 |
= 4 |
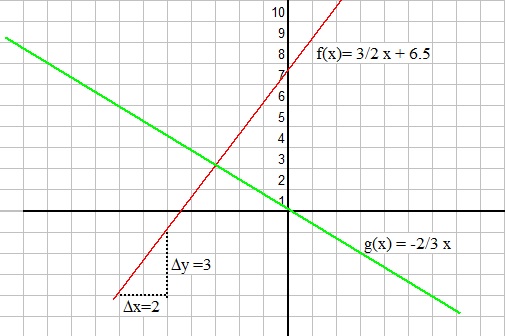
| slope= |
Δy -- Δx |
| y = ax + b | = | slope * x + b | = |
Δy -- x Δx |
+ b |
| slope= |
1 - 4 |
| x: | y: |
| 1 | 4 |
| 2 | 6 |
| 3 | 8 |
| 4 | 10 |
|
Δy -- Δx |
|
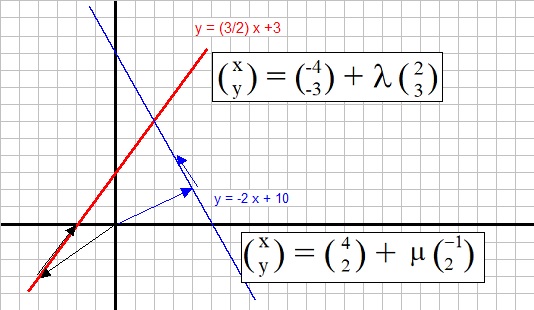
┌ x ┐ └ y ┘ |
= |
┌ -4 ┐ └ -3 ┘ |
+ | λ |
┌ 2 ┐ └ 3 ┘ |
|
┌ 0 ┐ └ 3 ┘ |
= |
┌ -4 ┐ └ -3 ┘ |
+ | 2 |
┌ 2 ┐ └ 3 ┘ |
|
┌ x ┐ └ y ┘ |
= |
┌ 4 ┐ └ 2 ┘ |
+ | μ |
┌ -1┐ └ 2 ┘ |
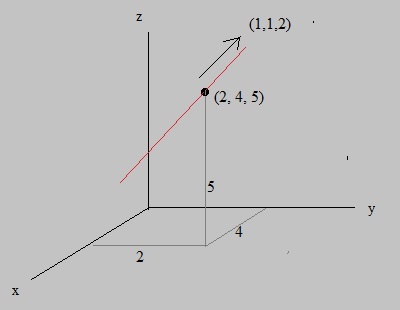
|
┌ x ┐ │ y │ └ z ┘ |
= |
┌ 2 ┐ │ 4 │ └ 5 ┘ |
+ | λ |
┌ 1 ┐ │ 1 │ └ 2 ┘ |
|
┌ x ┐ └ y ┘ |
= |
┌ -4 ┐ └ -3 ┘ |
+ | λ |
┌ 2 ┐ └ 3 ┘ |
|
┌ x ┐ └ y ┘ |
= |
┌ 4 ┐ └ 2 ┘ |
+ | μ |
┌ -1┐ └ 2 ┘ |
|
┌ x ┐ └ y ┘ |
= |
┌ -4 ┐ └ -3 ┘ |
+ | 3 * |
┌ 2 ┐ └ 3 ┘ |
= |
┌ -4 ┐ └ -3 ┘ |
+ |
┌ 6 ┐ └ 9 ┘ |
= |
┌ 2 ┐ └ 6 ┘ |
| A = |
┌ a ┐ └ b ┘ |
| B = |
┌ c ┐ └ d ┘ |
| A = |
┌ 1 ┐ └ 2 ┘ |
| B = |
┌ 3 ┐ └ -2┘ |
| A = |
┌ 1 ┐ └ 2 ┘ |
| AP = |
┌ -2┐ └ 1 ┘ |
| A = |
┌ a ┐ └ b ┘ |
| B = |
┌ -b┐ └ a ┘ |